Algorithmics

Defining functions

• A function is a reusable piece of algorithm
• It is mandatory for code readability and maintainability
• Function declaration :

  Function Integer factorial(input as Integer)
      Variable ... //local variables here
      BeginFunction
          ... // write the code here
          Return ... //return an integer value
      EndFunction
              

⚙ Exercises

Implement the factorial in a reusable function

Bonus : implement factorial in 3 different ways

Data Structures : Arrays

• Data need to be stored in more than one variables sometimes
• Thanks to arrays, it is possible
• Arrays will store a list of values, each value is made available through indexes

demo on draw.io

Arrays : example

Hereafter is the calculus of the average grade of a class

        //program that will calculate the average grade
        Variable grade as Integer[11]
        Variable i,avg,sum as Integer
        Begin
            For i <- 0 to 10
              Display "write grade #" + i
              Read grade[i]
            EndFor
            sum <- 0
            For i <- 0 to 10
              sum <- sum + grade[i]
            EndFor
            avg <- sum / 11
        End
    

⚙ Exercises

What will this algorithm produce?

        Variable NB as Integer[5]
        Variable i as Integer
        Begin
            For i <- 0 to 4
                NB[i] <- i * i
            EndFor
            For i <- 0 to 4
                Display NB[i]
            EndFor
        End
    

⚙ Exercises

What will this algorithm produce?

        Variable N as Integer[6]
        Variable i,k as Integer
        Begin
            N[0] <- 1
            For k <- 1 to 5
                N[k] <- N[k-1] + 2
            EndFor
            For i <- 0 to 5
                Display N[i]
            EndFor
        End
    

n-dimensions Arrays

This is the representation of a matrix

demo on draw.io

⚙ n-dimensions Arrays : exercises

        Variable T as Integer[4][2]
        Variables k,m as Integer
        Begin
            For k <- 0 to 3
                For m <- 0 to 1
                    T[k][m] <- k + m
                EndFor
            EndFor
            For k <- 0 to 3
                For m <- 0 to 1
                    Display T[k][m]
                EndFor
            EndFor
        End
    

Exercise : Sorting cards

take the cards in that order: 7, 3, 5, 9, Jack (11), King (13), 6

write an algorithm that will display the cards in ascending order (using a function)

Exercise : Wordsearch Problem

Write an algorithm. that will be able to find the following words in the table on the right:

T G C P N I H P L O D F P I
H N E I N T F G P A N D A M
A F H L R A U N I U G N E P
T C R P R I O R T I G E R L
Ε Ε Α O G O Τ Ε Τ Α Ε Ε Ε D
E P R I G A I O F L L E S O
H L L Y O D O A I F E I U G
C O E G T N C D G P A H O P
T M F P I O O A L I L R M O
B O M L H C W O I N L O I R
E N E C O A D O O T I L N G
A K E R E E N I I S C R A G
R E C H R R L I I E F O D N
I Y E R A T A N A T N R L B
   

More complex (custom) data structures

Arrays can be limited because:

• they have a fixed dimension ("extending" the array dimension is equivalent to make a full copy of it)
• as a consequence of the fixed dimension, insertion in the middle of an array is not easy
• the shape of an array does not fit all the situations (example: how to represent a company hierarchy with a single array?)

More complex (custom) data structures (2)

We need then custom data structures

• Dynamic lists, with different strategies
• Associative lists (aka Maps and Dictionaries)
• Trees
• Graphs

What will be in the list

Before we start with the ensemble considerations, we need to define what will be the content of each element in the list, dictionary or tree

Using pseudo-code, one can define a custom data structure thanks to the Structure keyword

        Begin Structure Node
            value as Integer
            next as Node
        End Structure
    

What's a linked (dynamic) list?

demo with draw.io, and expose the different strategies

• FIFO
• LIFO

Access is made by index

Exercise: implement FIFO and LIFO strategies using a linked list

take the same card game than in slide on card sorting

What's a Map/Dictionary/Registry?

• associates a unique key to some value (could be whatever type of value)
• Can be bidirectional (keys AND values are unique)
• Can have different strategies to store new key value pairs (order or usage first)

Access is made by key

Exercise: count the occurrences of each letter in the sentence "Hello World" using an associative array

The expected result is in the format :

"H" -> 1
"e" -> 1
"l" -> 3
 //...
    

Whats a tree?

• Its a hierarchical data structure, each node is composed of a set of children and a value
• If a node has no child, it's called a leaf
• The first node of the tree is called the tree root
• a child as exactly one parent node

Exercise

How would you display all the nodes? 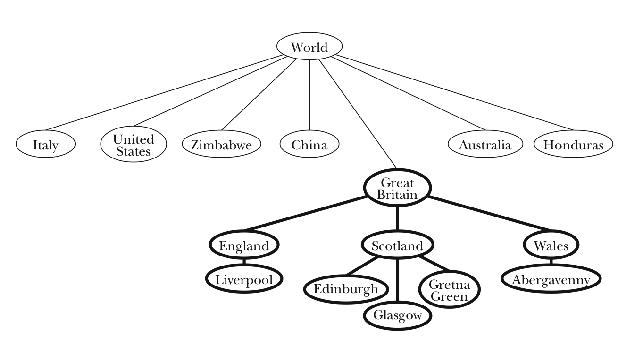credits berkeley.edu

What's a graph?

• It's a data structure that will allow to store values and relationships between node
• There's no hierarchy
• A graph can "cycle" meaning that there are looping references between nodes (should take care to manage that if you want to traverse the graph

Linked Lists - Structure Definition

A linked list is composed of nodes, where each node contains data and a reference to the next node

Begin Structure Node
    data as Integer
    next as Node
End Structure

Begin Structure LinkedList
    head as Node
    size as Integer
End Structure

Linked Lists - Insertion at Head (LIFO)

Function insertAtHead(list as LinkedList, value as Integer)
    Variable newNode as Node
    BeginFunction
        newNode.data <- value
        newNode.next <- list.head
        list.head <- newNode
        list.size <- list.size + 1
    EndFunction

// Example usage:
Variable myList as LinkedList
Begin
    myList.head <- null
    myList.size <- 0

    insertAtHead(myList, 5)  // List: 5
    insertAtHead(myList, 3)  // List: 3 -> 5
    insertAtHead(myList, 7)  // List: 7 -> 3 -> 5
End

Linked Lists - Traversal

To traverse a linked list, we start from the head and follow the next references

Function displayList(list as LinkedList)
    Variable current as Node
    BeginFunction
        current <- list.head

        While current is not null
            Display current.data
            current <- current.next
        EndWhile
    EndFunction

// Example:
Variable myList as LinkedList
Begin
    // ... (after inserting 7, 3, 5)
    displayList(myList)
    // Output: 7, 3, 5
End

Linked Lists - Search

Function Boolean search(list as LinkedList, value as Integer)
    Variable current as Node
    BeginFunction
        current <- list.head

        While current is not null
            If current.data = value Then
                Return True
            EndIf
            current <- current.next
        EndWhile

        Return False
    EndFunction

// Example:
Begin
    If search(myList, 3) Then
        Display "Value found!"
    Else
        Display "Value not found"
    EndIf
End

Linked Lists - Deletion

Function deleteValue(list as LinkedList, value as Integer)
    Variable current, previous as Node
    BeginFunction
        current <- list.head
        previous <- null

        While current is not null and current.data <> value
            previous <- current
            current <- current.next
        EndWhile

        If current is not null Then
            If previous is null Then
                list.head <- current.next
            Else
                previous.next <- current.next
            EndIf
            list.size <- list.size - 1
        EndIf
    EndFunction

Maps/Dictionaries - Structure Definition

A map associates keys with values using key-value pairs

Begin Structure KeyValuePair
    key as String
    value as Integer
End Structure

Begin Structure Dictionary
    pairs as KeyValuePair[100]
    count as Integer
End Structure

Maps/Dictionaries - Insertion

Function put(dict as Dictionary, key as String, value as Integer)
    Variable i as Integer
    Variable found as Boolean
    BeginFunction
        found <- False

        // Check if key already exists
        For i <- 0 to dict.count - 1
            If dict.pairs[i].key = key Then
                dict.pairs[i].value <- value
                found <- True
                Exit For
            EndIf
        EndFor

        // If not found, add new pair
        If not found Then
            dict.pairs[dict.count].key <- key
            dict.pairs[dict.count].value <- value
            dict.count <- dict.count + 1
        EndIf
    EndFunction

Maps/Dictionaries - Lookup

Function Integer get(dict as Dictionary, key as String)
    Variable i as Integer
    BeginFunction
        For i <- 0 to dict.count - 1
            If dict.pairs[i].key = key Then
                Return dict.pairs[i].value
            EndIf
        EndFor

        Return -1  // Key not found
    EndFunction

// Example:
Variable grades as Dictionary
Begin
    grades.count <- 0
    put(grades, "Alice", 95)
    put(grades, "Bob", 87)

    Display "Alice's grade: " + get(grades, "Alice")
End

Maps/Dictionaries - Traversal

Function displayAll(dict as Dictionary)
    Variable i as Integer
    BeginFunction
        For i <- 0 to dict.count - 1
            Display dict.pairs[i].key + " -> " + dict.pairs[i].value
        EndFor
    EndFunction

// Example output:
// Alice -> 95
// Bob -> 87
// Charlie -> 92

Binary Trees - Structure Definition

A binary tree has nodes with at most two children (left and right)

Begin Structure TreeNode
    data as Integer
    left as TreeNode
    right as TreeNode
End Structure

Begin Structure BinaryTree
    root as TreeNode
End Structure

Binary Trees - Insertion

Function TreeNode insert(node as TreeNode, value as Integer)
    BeginFunction
        If node is null Then
            Variable newNode as TreeNode
            newNode.data <- value
            newNode.left <- null
            newNode.right <- null
            Return newNode
        EndIf

        If value < node.data Then
            node.left <- insert(node.left, value)
        Else
            node.right <- insert(node.right, value)
        EndIf

        Return node
    EndFunction

Binary Trees - In-Order Traversal

Visit left subtree, then node, then right subtree (produces sorted output for BST)

Function inOrderTraversal(node as TreeNode)
    BeginFunction
        If node is null Then
            Return
        EndIf

        inOrderTraversal(node.left)
        Display node.data
        inOrderTraversal(node.right)
    EndFunction

// Example for tree with values: 5, 3, 7, 1, 4
// Output: 1, 3, 4, 5, 7

Binary Trees - Pre-Order Traversal

Visit node first, then left subtree, then right subtree

Function preOrderTraversal(node as TreeNode)
    BeginFunction
        If node is null Then
            Return
        EndIf

        Display node.data
        preOrderTraversal(node.left)
        preOrderTraversal(node.right)
    EndFunction

// Example for tree with values: 5, 3, 7, 1, 4
// Output: 5, 3, 1, 4, 7

Binary Trees - Post-Order Traversal

Visit left subtree, then right subtree, then node

Function postOrderTraversal(node as TreeNode)
    BeginFunction
        If node is null Then
            Return
        EndIf

        postOrderTraversal(node.left)
        postOrderTraversal(node.right)
        Display node.data
    EndFunction

// Example for tree with values: 5, 3, 7, 1, 4
// Output: 1, 4, 3, 7, 5

Binary Trees - Search

Function Boolean search(node as TreeNode, value as Integer)
    BeginFunction
        If node is null Then
            Return False
        EndIf

        If node.data = value Then
            Return True
        EndIf

        If value < node.data Then
            Return search(node.left, value)
        Else
            Return search(node.right, value)
        EndIf
    EndFunction

Graphs - Structure Definition

A graph consists of vertices (nodes) and edges (connections)

Begin Structure GraphNode
    data as Integer
    neighbors as GraphNode[10]
    neighborCount as Integer
    visited as Boolean
End Structure

Begin Structure Graph
    nodes as GraphNode[20]
    nodeCount as Integer
End Structure

Graphs - Depth-First Search (DFS)

Explore as far as possible along each branch before backtracking

Function DFS(node as GraphNode)
    Variable i as Integer
    BeginFunction
        If node is null or node.visited Then
            Return
        EndIf

        Display node.data
        node.visited <- True

        For i <- 0 to node.neighborCount - 1
            DFS(node.neighbors[i])
        EndFor
    EndFunction

Graphs - Breadth-First Search (BFS)

Visit all neighbors at current depth before moving to next level

Function BFS(startNode as GraphNode)
    Variable queue as GraphNode[100]
    Variable front, rear, i as Integer
    Variable current as GraphNode
    BeginFunction
        front <- 0
        rear <- 0
        queue[rear] <- startNode
        rear <- rear + 1
        startNode.visited <- True

        While front < rear
            current <- queue[front]
            front <- front + 1
            Display current.data

            For i <- 0 to current.neighborCount - 1
                If not current.neighbors[i].visited Then
                    current.neighbors[i].visited <- True
                    queue[rear] <- current.neighbors[i]
                    rear <- rear + 1
                EndIf
            EndFor
        EndWhile
    EndFunction

⚙ Exercises - Linked Lists

• Implement a function to insert a node at the end of a linked list (FIFO)
• Write a function to find the length of a linked list without using a size variable
• Implement a function to reverse a linked list
• Write a function to find the middle element of a linked list

⚙ Exercises - Trees

• Write a function to count the total number of nodes in a binary tree
• Implement a function to find the height (maximum depth) of a binary tree
• Write a function to check if two binary trees are identical
• Implement level-order traversal (visit nodes level by level)

⚙ Exercises - Graphs

• Implement a function to detect if a graph has a cycle
• Write a function to find the shortest path between two nodes (using BFS)
• Implement a function to check if a graph is connected
• Write a function to count the number of connected components in a graph

Summary - Data Structures